| Sujet : Un peu de gymnastique pour les neurones Nouveau | De ON5WF Le 20-04-2014 à 17:36 sta |
|

Pour ceux qui ne sauraient pas quoi faire, voici un petit problème pas bien méchant.
| |
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De Pierre-Alexandre Le 20-04-2014 à 19:54 sta |
|
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De Jean-B Le 20-04-2014 à 20:25 sta |
|
Je dirais plutôt 100/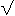 2 2
Numériquement égal, mais ...
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De guyguy Le 20-04-2014 à 21:28 sta |
|
Au pif, entre les 2/3 et les 3/4 environ 70.5 .
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De gentil Le 20-04-2014 à 23:07 sta |
|
Et bé moi, mes neurones sont cossards : je prends mon metrix, je mesure la tension et je tourne le potard.
La théorie ne marche jamais (ou presque) en radioélectricité...
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De pierre.ch Le 21-04-2014 à 00:46 sta |
|
Pierre Alexandre a donné la bonne réponse 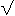 5000 5000
C'est normal c'est un Pierre 
Pierre
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De pierre.ch Le 21-04-2014 à 00:56 sta |
|
Quand à la théorie qui ne marche jamais ou plutôt qui ne concorde jamais exactement avec l'expérimentation...
Je citerais juste un prof de physique que j'ai eu il y a bien longtemps : " ce n'est pas grave que la théorie ne concorde pas avec l'expérimentation, l'essentiel c'est de pouvoir expliquer pourquoi elle ne concorde pas".
Pierre
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De jcj Le 21-04-2014 à 06:43 sta |
|
Personne pour résoudre ce petit problème... ?
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De ON5WF Le 21-04-2014 à 08:32 sta |
|

"La théorie ne marche jamais (ou presque) en radioélectricité..."
En radioélectricité comme dans toutes les sciences, la théorie est toujours basée sur des hypothèses qui ne "collent" jamais tout à fait à la réalité. Il y a donc toujours un écart plus ou moins grand entre les résultats expérimentaux et ce que prévoit la théorie. C'est précisément comme cela que la théorie peut (a pu ) progresser. Comme dit plus haut, l'essentiel est de pouvoir expliquer cet écart. 
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De gentil Le 21-04-2014 à 08:38 sta |
|
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De Jacques (webmestre) Le 21-04-2014 à 08:42 sta |
|
Y'a du Kirchhoff là dessous, avec la loi des noeuds et des mailles, mais c'est.... Pfouu, lointain.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De jcj Le 21-04-2014 à 09:21 sta |
|
Il suffit d'écrire que la résistance au dessus du curseur (R') est égale à la résistance en dessous du curseur (R'' en parallèle avec R).
Et en remplaçant R' = Rpot - R'' , il ne reste plus que R'' comme inconnue -> Equation du 2d degrés dans un cas particulier facile à résoudre.
Retour en classe de 2de.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De nanar Le 21-04-2014 à 09:30 sta |
|
1/R'=1/R''+1/R
donc 1/R'=1/R''+0,02
donc 1/R'-0,02 = 1/R''
donc(1/R'-0,02)-1/R''=0
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De grognon27 Le 21-04-2014 à 14:23 sta |
|
Bonjour
C'est une application basique du théorème de Thévenin avec comme tension intermédiaire U' = U*R"/(R' + R") et comme resistance interne r = R'*R"/(R'+R")... La tension UR=U'*R/(r+R)... En posant x = R"/Rpot la fraction utile du potentiomètre et compte tenu des constantes, on trouve x^2=1/2 soit x=71% ou 71 . .
Dans le cas général l'équation est :
x^2 + x ( R*U/(Rpot*UR) - 1 ) - R/Rpot = 0
Dans l'exemple cité le terme en x est nul (U/UR = 2 et Rpot/R = 2) et le calcul se simplifie fortement.
Bien à vous.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De baou_06 Le 21-04-2014 à 14:47 sta |
|
bien que ça se calcule aisément (en 7')
ce n'est pas de la théorie c'est tout simplement un calcul d'équation du second degré avec une seule racine R''² 5000 >> R'' =70.71 . .
je ne l'ai pas fait avec Thevenin , mais avec les courants .
merci ON5WF pour ce petit problème que tu as dû trouver sous un cocotier !
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De ON5WF Le 21-04-2014 à 16:49 sta |
|

Rien à ajouter à ce qui a été dit.
Sous le cocotier, il y avait aussi celui-ci.
| |
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De grognon27 Le 21-04-2014 à 17:16 sta |
|
Re-bonjour
En rentrant par le sommet A nous voyons 3 resistances identiques ainsi qu'en sortant par le sommet G. Il y a une symétrie parfaite qui se reproduit tous les tiers de tour. Ceci veut dire que si un courant I rentre dans le cube par le sommet A il se partage équitablement dans les 3 branches soit I/3. Les chutes de potentiel dans les 3 branches seront égales et les points B, E, D pourront ainsi être court-circuités sans effet. Le raisonnement vaut pour le sommet G et les points C, H, F. Ainsi nous nous retrouvons en partant de A et en mettant le réseau à plat avec 3 résistances en parallèle en série avec 6 résistances en parallèle en série avec 3 resistances en parallèle et nous sortons en G. Ce qui nous donne R/3 + R/6 + R/3 c'est-à-dire 5R/6, la résistance faisant 6  par hypothèse, la résistance résultante fera 5 par hypothèse, la résistance résultante fera 5  . Nous pouvons de la même manière calculer la résistance aux bornes d'une arête et aux bornes d'une diagonale d'un des carrés. Sur ces bonnes paroles je vais continuer ma déclaration d'impôts ce qui est une autre affaire. . Nous pouvons de la même manière calculer la résistance aux bornes d'une arête et aux bornes d'une diagonale d'un des carrés. Sur ces bonnes paroles je vais continuer ma déclaration d'impôts ce qui est une autre affaire.
Bien à vous.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De guyguy Le 21-04-2014 à 18:40 sta |
|
| |
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De guyguy Le 21-04-2014 à 18:54 sta |
|
Au pif : = 70.83333333 
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De pierre.ch Le 22-04-2014 à 02:42 sta |
|
La formule donnée pour le problème avec le rhéostat me semble bien inutilement compliquée.
On a tout simplement I = U/(Rh + R) ce qui est vrai pour Imin avec Rh à sa valeur maxi et aussi pour Imax avec Rh = 0.
On peut aussi écrire cette équation sous la forme: Rh = (U/I) - R si c'est Rh que l'on veut calculer en connaissant Imin
Mais bon pourquoi faire simple quand on peut faire compliqué 
Pierre
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De Florian . L Le 22-04-2014 à 03:00 sta |
|
Bonjour,
Oulalà!vous avez ressorti le livre de physique appliquée ... j'espère que vous avez prévu les cachets d'Aspirine pour le mal de crâne! 
Ceci dit, ça au moins le mérite d'entretenir ses connaissances afin d'éviter qu'elles sombrent dans l'oubli ...
Flo
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De ON5WF Le 24-04-2014 à 20:36 sta |
|

Un ptit dernier pour finir la semaine ?
| |
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 24-04-2014 à 21:02 sta |
|
allez, je m'lance, c'est les vacances mais bon ...
U1 = 180 V
U2 = 120 V
et ensuite U1 = U2 = 144 V 
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De jcj Le 24-04-2014 à 21:32 sta |
|
Cela semble très juste.
Petite question subsidiaire, avec les valeurs de fdevlos :
Avant de relier les condensateurs on avait donc :
Energie stockée dans C1 : 1/2 x C1 x U1² = 1/2 x 4µF x 180² = 64,8 mJ
Energie stockée dans C2 : 1/2 x C2 x U2² = 1/2 x 6µF x 120² = 43,2 mJ
Total : 108 mJ
Après liaison des condensateurs, on se trouve avec un condensateur de 10µF chargé à 144 V, soit une énergie : 1/2 x 10µF x 144² = 103,68 mJ
Perdu : 108-103,68 = 4,32 mJ
Normal ? Si oui ou est passé cette énergie ?
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De grognon27 Le 24-04-2014 à 21:57 sta |
|
Bonjour
Schéma 1 :
La tension U(C2) = U*C1/C1+C2 = 0,6*U = 180 V
La tension U(C1) = U*C2/C1+C2 = 0,4*U = 120 V.
Schéma 2 :
Chaque condensateur a une énergie potentielle du type (1/2) * C * U^2.
A la fermeture de l'interrupteur il y aura un transfert de charge entre C1 et C2 sans création ni perte d'énergie (ce qui n'est malheureusement pas possible !).
W(C1) = 0,5 * 6 * (120) ^ 2 = 43200 µJ
W(C2) = 0,5 * 4 * (180) ^ 2 = 64800 µJ
W(C1 + C2) = 108000 µJ énergie potentielle à la fermeture de l'interrupteur.
(1/2) * (C1 + C2) * V ^ 2 = 108000 µJ avec C1 + C2 = 10 µF ceci entraîne que V = 147 V.
Discussion : Bien sûr tout cela n'est que théorie. Il est bien sûr interdit de fermer l'interrupteur car le courant de circulation deviendrait infini. Il nous faut admettre que le circuit à une résistance non nulle qui consommera une partie de l'énergie et par conséquent la tension finale V sera inférieure à 147 volts.
Bon qu'en pensez-vous ?
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 24-04-2014 à 21:58 sta |
|
probablement dissipée dans une erreur de calcul !
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 24-04-2014 à 22:15 sta |
|
<<La tension U(C2) = U*C1/C1+C2 = 0,6*U = 180 V
La tension U(C1) = U*C2/C1+C2 = 0,4*U = 120 V.>>
Attention, c'est C1 qui vaut 4 µF ... donc plutôt U(C1)=180 V et U(C2)=120 V.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De grognon27 Le 24-04-2014 à 22:24 sta |
|
Re-bonsoir
Euh oui ! C'est le condensateur le plus petit qui a le plus de tension à ses bornes. Donc si C1 fait 4 µF il a bien 180V. C'est une erreur de plume, mais ça ne change pas le raisonnement. Ecrire des équations sur cet éditeur est un peu galère même si nous faisons attention... ce qui n'est pas suffisant. Donc merci pour la correction. A tous nous allons finir pas y arriver.
Cordialement.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 24-04-2014 à 22:32 sta |
|
pour la deuxième config, j'étais plutôt parti sur la conservation de la charge d'où
U=(C1xU1+C2xU2)/(C1+C2)=144 V, ça marche pas donc ... ne 
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De bthiry Le 25-04-2014 à 00:31 sta |
|
n'y a t'il pas dissipation d'énergie lors du transfert de charges entre les 2 condensateurs ?
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De pierre.ch Le 25-04-2014 à 01:14 sta |
|
fdevlos a juste fait une petite erreur de calcul ou une petite erreur en tapant la valeur arrondie du résultat.
U dans le schéma 2 vaut environ 147V (146,969384...................  ) et là l'énergie emmagasinée dans le premier montage se retrouve bien dans le second. ) et là l'énergie emmagasinée dans le premier montage se retrouve bien dans le second.
Pierre
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De jcj Le 25-04-2014 à 07:00 sta |
|
Je pense que fdevlos à raison. Quand on relie les 2 condensateurs, la charge se conserve (pas de raison qu'il en soit autrement). La tension commune sera bien de 144 V.
Par contre, on perd bien de l'énergie (4,32mJ), soit dans l'étincelle au moment de la fermeture de l'interrupteur (comme le signale grognon37 : pointe de courant infini si R = 0), soit dans la résistance totale du circuit.
On peut démontrer que cette puissance perdue par effet joule lors de la fermeture de l'interrupteur est toujours la même, quelle que soit la résistance R du circuit (donc valable aussi dans le cas limite théorique : R = 0).
Beau petit exercice de math/physique...
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 25-04-2014 à 12:14 sta |
|
C'est exactement ça.
En plaçant une résistance R entre les deux condos sur la deuxième config,
on peut déterrminer la solution de l'équa. diff. du premier ordre
lors du transfert de charge. L'évolution de l'intensité dans le circuit serait :
i(t)=- U1(C2-C1)/(2RC2) x e^-(C1+C2)t/(RC1C2)
En intégrant la piuissance dissipée Ri^2 entre 0 et +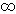 , on obtient , on obtient
une energie indépendante de R qui serait C1 U1^2 (C2 - C1)^2/(2 C2 (C1+C2))
ce qui donne 4,32 mJ.
Ouf, le perte est trouvée !
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De jcj Le 25-04-2014 à 13:19 sta |
|
Je trouve une expression des pertes Joules sous une forme différente, mais très certainement équivalente :
Pj = 1/2 x Ceq x (U1-U2)²
Ceq = Condensateur équivalent à C1 et C2 en série (2,4µF).
Cela ce présente bien sous la forme d'une énergie perdue par un condensateur. Comme si le condensateur équivalent série avait été chargé sous (U1-U2) = 60V et avait perdu cette énergie.
Et c'est bien cela, en y réfléchissant un peu, on pouvait écrire directement les pertes sous cette forme sans intégration. Les 2 condos en série formaient bien un condensateur de 2,4µF, chargé sous 60V et que l'on a court-circuité.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 25-04-2014 à 17:56 sta |
|
les raisonnements les plus simples sont en effet toujours les plus élégants.
Pour "amortir" le calcul différentiel, quelques évolutions (charges, tension, intensité)montrant la convergence vers le cas limite R=0 (1000  , 800 , 800  , 600 , 600  , ... ) -> , ... ) ->
Sais pas si on a fait le tour du problème, en tous cas ça fera un bon exo ...
| |
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 25-04-2014 à 18:32 sta |
|
petite erreur, l'évolution de u2 n'est pas la même que celle de u1, la voici ->
Les deux convergent bien vers 144 V.
| |
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De pierre.ch Le 25-04-2014 à 23:51 sta |
|
Pertes par effet Joule????
Dans le problème purement théorique posé elles n'existent pas . Les composants (fils conducteurs et condensateurs ) sont supposés idéaux donc ne présentant aucune résistance électrique : R fils conducteurs = 0 et condensateurs idéaux (éléments purement capacitifs) pas de résistance série ou de fuite (ni même d'effet de self ).
Dans ce cas (composants idéaux) l'énergie est conservée quand on passe du premier montage au deuxième montage puisqu'il n'y a pas de perte par effet Joule ni de pertes magnétiques ni ....
Dans le premier montage l'énergie emmagasinée est bien de 0,108J soit:
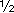 C1 U1² + C1 U1² + 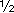 C2 U2² = 0,108J C2 U2² = 0,108J
avec C1 =4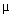 F C2 = 6 F C2 = 6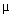 F U1 = 180V U2 = 120V F U1 = 180V U2 = 120V
ou bien 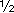 Cequ U² = 0,108J Cequ U² = 0,108J
avec Cequ = C1 en série avec C2 Cequ = 2,4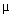 F U = 300V F U = 300V
Dans le deuxième montage l'énergie étant conservée on a:
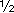 Ceq V² = 0,108J Ceq V² = 0,108J
avec Ceq = C1 en parallèle avec C2 Ceq = 10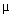 F V tension (dont on recherche la valeur) aux bornes de l'ensemble C1 C2 F V tension (dont on recherche la valeur) aux bornes de l'ensemble C1 C2
ce qui donne V² = 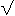 21600 soit V = environ 147V ( 146,969384 ...) 21600 soit V = environ 147V ( 146,969384 ...)
Pierre
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De jcj Le 26-04-2014 à 06:06 sta |
|
Pas d'accord...
Bien sur qu'un circuit avec résistance nulle ça n'existe pas, mais cela ne veut pas dire qu'il n'y aurait pas de pertes Joule.
R = 0, mais i = infini.
Et 0 x infini = quelque chose d'indéterminé, mais quelque chose...
Sinon, le même raisonnement appliqué à un condensateur chargé que l'on court-circuite par un fil de résistance nulle, ne se déchargerait jamais.
C'est d'ailleurs le cas ici, avant fermeture de l'interrupteur, l'ensemble constitue bien un condensateur de 2,4 µF, chargé à 60 V, et qui va se décharger à la fermeture de l'interrupteur qui le met en court-circuit.
Ce qui redonne bien les 4,32 mJ perdus et 144 V de tension commune.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 26-04-2014 à 07:28 sta |
|
D'accord avec jcj, d'ailleurs c'est ce que dit la résolution de l'équation
différentielle satisfaite par les charges des condos dans l'hypothèse
d'une conservation globale de ces charges.
La puissance instantanée Ri^2 dissipée pour différentes valeurs de R insérée
dans le circuit ->
Ce qui est remarquable, c'est que la surface sous chacune des courbes est identique.
L'énergie dissipée ne dépend pas de R comme le suggérait jcj.
Lorsque R est proche de 0, en plus de l'effet Joule sur les contacts de l'interrupteur
une bonne partie de l'energie doit probablement être évacuée sous forme de rayonnement
électromagnétique par l'étincelle.
| |
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De grognon27 Le 27-04-2014 à 14:39 sta |
|
Bonjour
Bon, je crois que nous avons fait le tour de la question. Un problème me taraude encore :
Quand nous chargeons un condensateur C sous une tension U via une résistance R le générateur employé fournit une énergie W = C*U^2 ; si nous déchargeons ce condensateur dans une autre résistance, le condensateur ne fournit plus que la moitié de cette énergie.
Question : N'y aurait-il pas une façon plus économique de charger le même condensateur sous la même tension ?
Bien à vous.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 27-04-2014 à 17:12 sta |
|
bonjour,
question probablement bête, mais pourquoi W = C*U^2 ?
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 27-04-2014 à 17:52 sta |
|
ah, oui, après calcul :
i(t) = U*e^( -t/RC) / R
et en intégrant entre 0 et +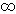 la puissance instantanée P = U x i(t), on obtient bien la puissance instantanée P = U x i(t), on obtient bien
W = CU^2
Par contre, si on intègre la puissance Ri^2 dissipée dans la résistance, on obtient CU^2/2.
La moitié de l'énergie produite serait dissipée dans la résistance et ceci quelque soit sa valeur, l'autre moitié serait stockée dans le condo
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De jcj Le 27-04-2014 à 18:35 sta |
|
"... le condensateur ne fournit plus que la moitié de cette énergie.
Question : N'y aurait-il pas une façon plus économique de charger le même condensateur sous la même tension ?"
La perte d'énergie lors de la charge (moitié de l'énergie perdue dans R), est du à la présence de R, c'est une évidence.
Si on suppose que R=0, il y a quand même perte d'énergie s'il y a des discontinuités de tension qui entrainent des pointes de courant infinie. C'était le cas du problème précédent.
S'il n'y a ni résistance dans le circuit, ni discontinuité de tension, il n'y a pas de pertes. C'est par exemple le cas d'un condensateur relié au réseau alternatif sinusoïdal, qui n'arrête pas de se charger et de se décharger sans aucune perte.
fdevlos doit pouvoir nous le démonter avec un calcul intégral.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De omer_gennius Le 27-04-2014 à 18:57 sta |
|
Le diviseur R' R" pour avoir 50V au milieu il faut R'=R" = 50 ohm.
Si la résistance R" est composée de 2 résistances // on a un problème vu que la nouvelle résistance =50 ohm. Donc première solution R" est infinie et on a bien 50V mais inutile de mettre un potar, on le positionne au milieu et on ne branche pas l'extrèmité. Ou on néglige le courant dans la 50 ohm de charge dans les calculs ce qui veut dire un potar dont la résistance totale est au moins dix fois plus petite que la charge (5 ohm).
LOL
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 27-04-2014 à 19:15 sta |
|
Bon allez, plus que quelques heures de vacances.
En régime sinusoïdal établi, pour R=0, et une pulsation 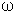 , ,
on a pour un générateur délivrant u(t) = U0cos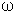 t : t :
q(t) = U0 C cos 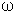 t puis i(t) = - U0 C t puis i(t) = - U0 C 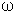 sin sin 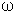 t d'où la puissance t d'où la puissance
instantanée :
p(t) = - U0^2 C 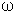 sin sin 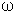 t cos t cos 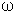 t = -1/2 U0^2 C t = -1/2 U0^2 C 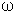 sin 2 sin 2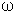 t t
En intégrant cette puissance sur une période (0 -> 2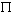 / /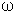 ), on obtient bien une énergie nulle. ), on obtient bien une énergie nulle.
En revanche, à la mise sous tension, on a un régime transitoire qui doit probablement
conduire à des pertes ...
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De grognon27 Le 27-04-2014 à 22:45 sta |
|
Bonsoir
Je m'interrogeais précédemment pour trouver un système de charge plus efficace qu'une source de tension et une résistance.
J'ai ainsi pris comme exemple une source de courant I qui, débitant sur notre condensateur C, génère une rampe linéaire de tension d'équation U(t) = (1/C) * I * t ...
A chaque intervalle de temps l'énergie fournie par la source de courant est
dW = U(t) * I * dt ou (1/C) * I ^ 2 * t * dt
en intégrant sur 0 --> T il vient W = (C/2) * (I*T/C) ^ 2 = (1/2)*C*U(T)^2 qui est l'aire de la surface triangulaire sous la courbe de charge.
En bref l'énergie fournie par la source de courant I et l'énergie disponible aux bornes du condensateur sont les mêmes = 0,5 CU2.
Il reste à trouver une source de courant pratique qui ne consomme pas d'énergie, ce qui n'est pas demain la veille.
Bien à vous.
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 28-04-2014 à 05:40 sta |
|
Bonjour,
<< U(t) = (1/C) * I * t >> : peut-être prévoir dans ce cas un générateur
de courant très faible ou un moyen de couper l'alimentation assez rapide
pour ne pas dépasser la tension de claquage du condo.
Bonne journée
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De jcj Le 28-04-2014 à 06:50 sta |
|
Le condensateur par lui même n'est pas responsable des pertes d'énergie, quelle que soit la forme de la tension à ses bornes (à condition que la dérivée de la tension existe : pas de discontinuité).
L'énergie qu'il stocke ou qu'il perd ne dépend que des tensions initiale et finale à ses bornes. (démo ->).
S'il y a des pertes, elles ne proviennent que de la source de tension ou de courant.
| |
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 28-04-2014 à 12:52 sta |
|
ça a le mérite d'être clair, ça permet surtout de répondre à la question :
<<N'y aurait-il pas une façon plus économique de charger le même condensateur sous la même tension ?>>.
Sans faire appel à l'artifice d'un générateur de courant, il suffit de connecter
le condo à un générateur de tension variable qui partiraît de 0 V.
Pour reprendre l'idée de grognon27, par exemple une rampe : U(t) = 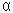 t, en remplaçant t, en remplaçant
dans son développement I/C par 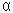 quelconque, on arrive au résultat de perte nulle quelconque, on arrive au résultat de perte nulle
en l'absence de R.
Comme quoi, rien ne sert de courir, il faut arriver à temps ou comment allier philosophie et condensateurs.
En revanche, si on introduit une résistance R dans le circuit et qu'on alimente avec une
telle rampe de tension, on obtient une perte qui dépend de R contrairement
à l'échelon de tension pour lequel la perte dans R était toujours égale à la valeur stockée dans C.
L'équa. diff. avec second membre non constant s'intègre aussi sans difficulté par transformée de Laplace, on obtient : ( i(t)=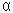 C+ C+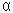 RC^2e^(-t/RC) ) RC^2e^(-t/RC) )
On enfonce probablement des portes ouvertes, mais il est parfois bon de revenir
aux fondamentaux comme dirait Laporte (Bernard) 
|
|
| Sujet : Un peu de gymnastique pour les neurones Nouveau | De fdevlos Le 28-04-2014 à 13:47 sta |
|
erreur, problème d'homogénéité, c'est plutôt : i(t) = 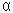 C(1-e^(-t/RC)) C(1-e^(-t/RC)) 
|
|
|


 Journaux du site au 22/08/2022 à 10:26
Journaux du site au 22/08/2022 à 10:26


 2
2

 .
.


 , on obtient
, on obtient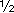 C1 U1² +
C1 U1² + 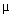 F C2 = 6
F C2 = 6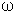 ,
,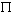 /
/
 t, en remplaçant
t, en remplaçant
